RESISTENCIA ELÉCTRICA DE LOS MATERIALES
Resistencia de un conductor
Si
midiésemos la resistencia de un conductor de cobre de un metro de longitud y de
un milímetro cuadrado de sección, obtendríamos un resultado de 0.017Ω Este resultado nos indica que cada metro de
conductor de cobre de un milímetro cuadrado de sección, la resistencia del
mismo será de 0.017 Ω
La resistencia
de un conductor aumenta con su longitud, es decir a mayor longitud, mayor será la resistencia. Así por ejemplo, si midiésemos la resistencia de un conducto de 2
metros de cobre de 1 mm2, observaríamos que la
resistencia ha aumentado al doble (0.034 Ω)
La fórmula general para calcular la resistencia de
cualquier tipo de conductor podría quedar así:
La resistencia es igual a la resistividad por la longitud
dividida por el área.
Donde R
es el ohm Ω, ρ= Resistividad del material (W.m), L=
Longitud en metros del conductor, S=
Área transversal del conductor en mm cuadrados. La resistividad
eléctrica es una constante que depende de cada material. A
continuación daremos algunos valores:
Los conductores son materiales que permiten que fluya corriente por
ellos con facilidad. La plata, el cobre y el aluminio son ejemplos de buenos
conductores.
Los aislantes son materiales que no permiten que fluya corriente por
ellos. El hule, el vidrio, la mica y la mayoría de los plásticos son ejemplos
de aislantes.
La resistencia de un alambre varía directamente con su longitud e
inversamente con el área de su sección transversal. La resistencia también
depende del material con el cual este hecho el conductor y de la temperatura.
Para medir el calibre de alambre su usa el American Wire Gage (AWG).
Los aislantes pueden soportar voltajes hasta de un valor crítico. Si
su voltaje es igual o mayor que el crítico,
los aislantes presentan una ruptura y permite el flujo de corriente por
arco eléctrico.
El voltaje de ruptura de un aislante depende de su material.
La resistividad de un buen
conductor es muy baja y la de un aislante muy alta. A continuación veremos un problema de ejemplo.
Calcular la resistencia de un conductor de cobre de 2 km de largo y 4 mm
de diámetro. Su Resistividad es de 1.72 X 10-2 Ω.mm2/m
La longitud de 2 km la pasamos a
metros y nos da 2000 metros. Por otra parte con el diámetro podemos calcular la
superficie o sección del conductor en mm cuadrados.
A = 3.14X 16 mm2 / 4 A = 12.56 mm2
Ahora si podemos calcular la resistencia del conductor.
R = (1.72 X 10-2 Ω.mm2/m) x(
2000 mts / 12.56 mm2 )
Influencia de la temperatura sobre la resistividad
Por lo general, la resistencia aumenta con la temperatura en los conductores metálicos. Este aumento depende del incremento de temperatura y de la materia de que esté construido dicho conductor.
Material
|
|
Oro
|
0.0035
|
Plata
|
0.0036
|
Aluminio
|
0.00446
|
Cobre
|
0.0039
|
Estaño
|
0.0044
|
Constantán
|
0.0001
|
Wolframio
|
0.0005
|
Hierro
|
0.00625
|
Ferroniquel
|
0.00093
|
Maillechort
|
0.00036
|
Con
esta expresión se puede calcular la resistencia a una temperatura dada(R0),
conociendo la temperatura de la resistencia en frío (R0), la elevación de la temperatura
y el coeficiente de temperatura ( α ),
que
será diferente para cada material.
Una lámpara incandescente
9 v
Una lámpara de 120 V 60
W ac
a).-Toma
la lámpara de 9 V y mide con el óhmetro su resistencia en frío. Seguidamente, conecta la lámpara a una fuente a 9V y
mediante un amperímetro y un voltímetro determina los valores de Intensidad
y con ellos determina los valores
de la resistencia óhmica del filamento
en caliente.
b).-Repite
el experimento para la lámpara de 120 V 60 W, aplicando la ley de Ohm Compara los resultados obtenidos ¿Obtuviste los mismos resultados en los dos
casos práctico y teórico?
Seguro
que no. Al medir la resistencia con
el Óhmetro, la lámpara está apagada y,
por lo tanto el filamento se encuentra frío, es decir, a temperatura ambiente. Por otro lado cuando aplicamos la ley de
Ohm para calcular la resistencia, se hace con los datos de correspondientes al
estado de encendido de la lámpara. Hay
que tener en cuenta que en ese estado, el filamento se encuentra a una
temperatura de unos 2000
. Y es que la
resistencia eléctrica se eleva sustancialmente en casi todos los conductores al
elevarse su temperatura, de aquí
que en una lámpara
incandescente la resistencia en
frío sea muy inferior a cuando está
caliente.
Resuelva el
ejercicio propuesto:
¿Cuál será el aumento de temperatura que
experimentara una lámpara incandescente con filamento de wolframio, si al medir
su resistencia a temperatura ambiente ( 20°C) obtuvimos un resultado de 358
,
habiéndose calculado una resistencia en caliente de 807Ω
Haga comentarios sobre los
resultados obtenidos en los
procedimientos.
______________________________________________________________________________________________________
______________________________________________________________________________________________________
______________________________________________________________________________________________________
______________________________________________________________________________________________________
______________________________________________________________________________________________________
______________________________________________________________________________________________________
______________________________________________________________________________________________________
______________________________________________________________________________________________________
______________________________________________________________________________________________________
______________________________________________________________________________________________________
______________________________________________________________________________________________________
_____________________________________________________________________________________________________
Práctica # 5
RESISTENCIAS
1. Conocer el Código de Colores para
Resistencias.
2. Conocer el funcionamiento del multímetro digital.
El Código
de Colores para Resistencias es una forma convencional de identificar los
valores de las resistencias utilizadas en circuitos electrónicos, ya que éstas
pueden ser demasiado pequeñas como para imprimir en ellas toda la información
necesaria para su utilización. Este código consta de varias bandas de colores
impresas en el cuerpo del resistor, cercanas a uno de los extremos, como se muestra
en la figura.
Cada color tiene una equivalencia numérica. La franja más cercana a la
orilla se considera la primera y representa el dígito más significativo, la
segunda franja representa el dígito menos significativo, la tercera nos indica
el multiplicador y la última, la tolerancia o el rango de variación que nos
asegura el fabricante. Todo esto puede apreciarse en la tabla:
El instrumento básico empleado para medir la Resistencia es el
Ohmímetro, compuesto generalmente de una fuente de voltaje, un medidor de
corriente y un selector de rangos de medición. En este curso, emplearemos un Multímetro
Digital, que es un instrumento que mide cantidades analógicas y las muestra en
forma digital. El multímetro recibe ese nombre porque no sólo sirve para medir
resistencia, sino también corriente y voltaje (en CA o CD), con diferentes
escalas.
20 resistencias de diferentes valores
2 cables de conexión con caimanes
1. Utilizando cada una de las 20 resistencias solicitadas para esta
práctica, complete la tabla 5-2, primero con los colores de cada franja,
después con el valor de la resistencia y la tolerancia.
2. Siguiendo las indicaciones
de su maestro, utilice el multímetro digital para medir el valor de cada
resistencia. Anote los valores en la columna correspondiente en la tabla 5-2.
Tabla
5-2
3. ¿Son aproximadamente iguales los valores medidos y los
nominales de las resistencias?
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
4. Si no es así, explique por qué.
________________________________________________________________________________________
________________________________________________________________________________________
________________________________________________________________________________________
________________________________________________________________________________________
________________________________________________________________________________________
Tabla 5-3
2. ¿Por qué las resistencias son de diferente tamaño?
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
3. ¿Cuáles son las que tienen mayor capacidad para disipar
calor?
________________________________________________________________________________
________________________________________________________________________________
¿Por qué?
_______________________________________________________________________________________
________________________________________________________________________________________
________________________________________________________________________________________
Práctica # 6
ARREGLOS DE RESISTENCIAS
1. Aprender a construir circuitos eléctricos
basándose en diagramas esquemáticos.
2. Calcular y medir la resistencia equivalente de resistencias conectadas
en serie, paralelo y serie-paralelo.
En esta práctica el alumno aprenderá a hacer conexiones basándose en un
diagrama de alambrado, lo que constituye el primer paso para interpretar
combinaciones más complejas.
Para hacer las conexiones, se utilizará el juego cables con caimanes.
También se harán cálculos de las resistencias equivalentes basándose en
la teoría y se usará equipo real para medir y comparar los resultados teóricos
y los experimentales. El método experimental es el mejor procedimiento de
comprobación o corrección de una teoría, de ahí la importancia del trabajo en
el laboratorio.
Como es poco probable que los resultados teóricos y experimentales
coincidan exactamente, usualmente se tendrá una diferencia o error entre ambos,
debida a factores tales como precisión de los instrumentos de medición, la
tolerancia de los componentes, el error humano en las lecturas de los
instrumentos, etc. La diferencia entre los valores teóricos y experimentales se
expresa casi siempre como un porcentaje.
En estas prácticas, es aceptable un
error del 10%.
Resistencias: 20 resistencias de
carbón, use en cada circuito las que se
indican.
Un multímetro digital, juego de
caimanes con cable.
1.
Examine la red de la figura 6-1. Calcule la resistencia equivalente
entre las terminales que se indican. Anexe sus cálculos al final de la
práctica.
El efecto de
conectar dos o más resistores en serie en un circuito cerrado que contiene una
fuente de voltaje V, es ofrece mayor resistencia a la corriente de la que
proporciona cualquiera de esos resistores en forma individual
El
valor de la resistencia total (RT ) de resistores conectados en serie también puede medirse en forma
directa con un óhmetro. Sin embargo, al
usar el óhmetro para medir la resistencia total de circuito en serie, la fuente
de alimentación se debe desconectar de
los resistores.
Si se
necesita obtener una resistencia de valor de RT mediante un conjunto
de resistores conectados en serie cuyos valores son R1, R2, R3
la combinación de resistores debe satisfacer la fórmula
2. Siguiendo las indicaciones
de su maestro, mida y anote el valor de la resistencia equivalente. Calcule el
porcentaje de error.
Valor
Calculado:
|
Valor
Medido:
|
% de
error:
|
Req =
____________
|
Req =
_____________
|
% e =
_____________
|
Una fórmula que expresa la relación entre la
resistencia total (RT) y R1, R2, R3,
etcétera. Cuando los resistores están conectados en paralelo es:
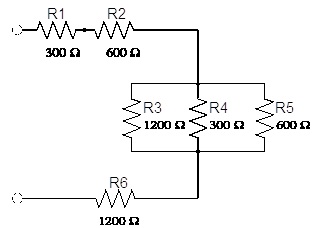
3. Repita los procedimientos 1 y 2 para cada una
de las figuras que siguen y complete la tabla 6-1
Diagrama 6-2 (Fig. 2-2)
Diagrama 6-3 (Fig. 2-3)
Diagrama 6-4
(Fig. 2-4)
Diagrama 6-5 (Fig. 2-5)
Diagrama 6-6
(Fig. 2-6)
TABLA 6-1
1. ¿Qué significa el término “Corto circuito”?
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
2. ¿Cuál es el valor de la resistencia de un corto circuito?
________________________________________________________________________________
________________________________________________________________________________
3. ¿Cuál es el valor de la resistencia de un circuito
abierto? ________________________________________________________________________________
________________________________________________________________________________
________________________________________________________________________________
4. Si sólo tuviera tres
resistencias de 300 Ω, tres de 600 Ω y tres de 1200Ω ¿cuáles serían las
conexiones que podría hacer para obtener equivalentes de 120Ω,
171.4Ω y 57.1Ω?
Dibuje las conexiones enseguida:
Práctica # 7
LEY DE OHM
1. Conocer el funcionamiento de la fuente de
alimentación.
2. Aprender a usar el multímetro para medir
corrientes y voltajes.
3. Comprobar experimentalmente la Ley de Ohm.
La Ley de Ohm establece que el voltaje entre los extremos de muchos
tipos de materiales conductores es directamente proporcional a la corriente que
fluye a través del material,
donde la constante de proporcionalidad R recibe el nombre de "resistencia".
La unidad de resistencia es el ohm, el cual es igual a 1 V/A y generalmente se
simboliza por una omega mayúscula, Ω.
Para comprobar experimentalmente la Ley de Ohm, aplicaremos voltajes o
corrientes conocidos a resistores como los usados en las prácticas anteriores,
y mediremos la respuesta. Con este propósito usaremos la fuente de 9 voltios y la de 1.5 voltios; y el
multímetro digital que habíamos usado anteriormente sólo para medir
resistencias; en esta práctica lo usaremos además para medir corrientes y
voltajes.
Para medir corrientes, el multímetro se tiene que conectar en serie con
el elemento cuya corriente se quiere obtener; de ese modo se estaría conectando
como amperímetro. Es importante hacer notar que para obtener una lectura
positiva, la flecha de corriente tiene que entrar por la terminal positiva del
medidor.
Para medir voltajes, el multímetro tiene que conectarse en paralelo con
el elemento cuyo voltaje se quiere obtener; de ese modo se estaría conectando
como voltímetro. Para obtener una lectura positiva, la polaridad de las
terminales del medidor tiene que coincidir con la polaridad asignada al
elemento en cuestión.
Lo
anterior puede observarse en el circuito que se muestra en la fig. 7-1. El
círculo con la letra "A" es el símbolo para un amperímetro; note que
se encuentra conectado en serie con la resistencia R. El círculo con la letra
"V" es el símbolo para un voltímetro; observe que se encuentra
conectado en paralelo con la resistencia R. Entonces, estos medidores nos
indicarán, respectivamente, los valores de la corriente y el voltaje de la
resistencia R.
FIG. 7-1
Resistencias: 20 resistencias de diferentes valores
Fuente de alimentación de 9 v y
1.5 voltios
1)
Mida y ordene las resistencias de mayor valor
a menor y anótelos en la tabla 7-1.
a. Examine el circuito de la figura 7-2. Y
realícelo usando la fuente de 9 V; calcule
la corriente I para cada uno de los 20 valores de
resistencia del paso anterior empezando
por la de mayor valor anote los resultado en la tabla 7-1
NOTA: Observe que no se especifican los medidores de corriente y voltaje. La
razón es que se utilizará el mismo multímetro para hacer todas las mediciones.
Su maestro le indicará como hacer cada medición. Para evitar cualquier problema
con las conexiones, obedezca todas las indicaciones de su maestro y espere su
autorización antes de energizar el equipo.
1.
Ahora
use la fuente variable de c.c en el
laboratorio y conecte el circuito de la figura 7-2 escoja una resistencia a su
gusto y déjela fija.
a) Cambie sucesivamente los voltajes en la fuente de
menor a mayor. Mida y anote en la tabla
7-2 la corriente para cada valor de voltaje de la fuente.
Resistencias
|
I medida
|
I calculada
|
% de error
|
comentario
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tabla 7-1
Voltajes
|
I medida
|
I calculad
|
Resistencia
|
comentario
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tabla 7-2
b) Calcule el porcentaje de error.
c) Grafique los resultados corriente contra resistencia
calculados y medidos.
3. Haga comentarios sobre las
gráficas que dibujó en los procedimientos 1, 2.
___________________________________________________________________________________________
___________________________________________________________________________________________
___________________________________________________________________________________________
___________________________________________________________________________________________
___________________________________________________________________________________________
___________________________________________________________________________________________
___________________________________________________________________________________________
___________________________________________________________________________________________
___________________________________________________________________________________________
___________________________________________________________________________________________
___________________________________________________________________________________________
___________________________________________________________________________________________
Práctica # 8
RESISTENCIAS EN SERIE, EN PARALELO Y SERIE PARALELO
1.- Calcular
la resistencia equivalente de varias resistencias conectadas en serie.
2.- Calcular
la resistencia equivalente de varias resistencias conectadas en paralelo.
3.- Calcular
la resistencia equivalente de
varias resistencias conectadas en serie-paralelo.
4.- Conocer
y aprender la función de las resistencias.
5.- Calcular
y medir la resistencia equivalente de las resistencias conectadas en serie,
paralelo y serie-paralelo.
6.- Aprender
a construir circuitos eléctricos desde simples a complejos de acuerdo con diagramas.
1.- Como
se expuso en la ley de Ohm, la resistencia es un elemento pasivo; es un
conductor que se opone en mayor o menor grado al paso de la intensidad de
corriente. Como en un circuito eléctrico
aparecen varias resistencias conectadas en :
serie, paralelo, o serie-paralelo, es necesario determinar su resistencia
equivalente:
a)
RESISTENCIAS EN SERIE.
Cuando dos o más resistencias se conectan en
serie, equivalen a una resistencia que
es igual a la suma de las resistencias parciales, Fig. 8-1.
Fig. 8-1
REquivalente = R1
+ R2 +
R3 +· . . . Rn
Cuando dos o más resistencias se conectan en
paralelo, la inversa de la resistencia equivalente es igual a la suma de las
inversas de las resistencias parciales, Fig. 8-2.
Fig. 8-2
Caso
de tres resistencias
Por lo que en
forma general la resistencia equivalente de resistencias en paralelo es igual:
al producto de todas las resistencias dividida por la suma de los productos de
las resistencias parciales (los productos serán de todas las resistencias
combinadas menos una de la resistencias parciales en forma secuencial).
La resistencia
equivalente será menor que la menor de las parciales.
c)
RESISTENCIAS SERIE-PARALELO
La resistencia equivalente de un circuito
serie-paralelo es igual a la suma de las resistencias en serie más la
resistencia equivalente de las resistencias en paralelo. Fig. 8-3.
Fig. 8-3
Por lo que se
deduce que aplicando las expresiones de (a) y (b), se obtiene la resistencia
equivalente de este tipo de arreglo.
Asistir al Laboratorio de Maquinas
eléctricas.
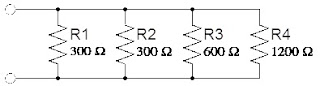
El módulo de resistencias (MC-5020) está formado
por nueve resistencias de potencia, en tres secciones iguales. Cada sección tiene dos terminales, tres
resistencias de 300, 600 y 1200 ohms y sus respectivos interruptores de tal
manera que pueden quedar conectadas a las terminales una, dos y tres en
paralelo. Si se utilizan las tres
secciones uniendo sus terminales se pueden conectar hasta nueve resistencias en
paralelo. Fig. 8-4
Fig. 8-4
Para medir la resistencia
se utiliza el óhmetro. El óhmetro se
basa en el principio de que aplicando una tensión de c.c. a un amperímetro
conectado en serie con la resistencia, su desplazamiento inverso es
proporcional a dicha resistencia en función de la intensidad de corriente que
circula.
No se requiere un óhmetro especial, ya que existen varios instrumentos
que miden resistencia del tipo multímetro, bien sea analógico (con medidor de
aguja) o digitales.
Los diagramas eléctricos de
circuitos, generalmente se presentan en una forma clara, pero en la práctica el
circuito físico real es diferente, por lo que se hace necesario aprender a
interpretarlos, a fin de que las conexiones sean las correctas.
Los resultados teóricos por lo
general no son iguales a los obtenidos en la práctica, sobre todo con
instrumentos analógicos o elementos pasivos que no tienen una precisión exacta;
pero sí deben obtenerse resultados aproximados con errores tolerables.
La diferencia entre los valores
teóricos y los experimentales, se expresan en porcientos.
Donde: Vt = valor teórico
El error puede ser positivo o
negativo y un valor aceptable es de 10%.
PARTES Y EQUIPO REQUERIDO
DESCRIPCION
|
Nº. DE PARTE
|
Resistencias
|
MC-5020
|
Cables de conexión
|
WIR-5029
|
Ohmetro
|
No
Incluido
|
1.- En
base a las expresiones dadas en resumen
teórico, calcule la resistencia de
los circuitos siguientes:
a-1) Req = _________________
a-2) Req=_________________
a-3) Req = ________________
b-1).- Req = _________________
b-2).- Req = _________________
b-3).- Req = _________________
b-4).- Req = _________________
b-5).- Req = _________________
c-1).- Req = _________________
c-2).- Req = _________________
c-3).- Req = _________________
2.- Medición
de resistencia utilizando el módulo de
resistencias (MC-5020).
a)
Examine las resistencias del módulo (MC-5020),
poniendo especial atención en los valores de las resistencias, los
interruptores de palanca, las terminales de conexión y las conexiones indicadas
en el diagrama del tablero. Observe que
se divide en tres secciones iguales con tres resistencias cada
uno de 300, 600 y 1200. Observe que cada resistencia tiene un interruptor de palanca para conectar estas a
las terminales.
b)
Utilizando un óhmetro mida cada una de las
resistencias cerrando el interruptor (palanca hacia arriba), teniendo abierto
los otros interruptores (palanca hacia abajo).
Anote los resultados en la tabla 8-1 y compárelos con sus valores
nominales.
Valor
Nominal
|
1200
|
600
|
300
|
1200
|
600
|
300
|
1200
|
600
|
300
|
Lectura
|
|
|
|
|
|
|
|
|
|
Tabla 8-1
Req (Calc) =
_________________
Req (Med) =
__________________
Req (Calc) =
_________________
Req (Med) =
__________________
Req (Calc) =
_________________
Req (Med) =
__________________
Req (Calc) =
_________________
Req (Med) =
_________________
Req (Calc) =
_________________
Req (Med) =
__________________
1.- Conecte
en serie las resistencias, calcúlelas y mídalas.
2.- Conecte
en paralelo las resistencias, calcúlelas y mídalas.
3.- Conecte
en serie-paralelo las resistencias, calcúlelas y mídalas.
R eq =
_______________
LEYES DE KIRCHHOFF
1. Comprobar experimentalmente las Leyes de Kirchhoff.
Las Leyes de Kirchhoff
constituyen la base para el análisis de los circuitos eléctricos. Sus
conceptos básicos son tan amplios, que pueden aplicarse a cualquier circuito,
desde el circuito más sencillo, hasta la red más compleja.
Primera Ley: LEY DE CORRIENTES DE KIRCHHOFF: "La suma algebraica de
las corrientes que entran a (o salen de) una unión de dos o más elementos es
igual a cero".
Esto significa que la suma de las corrientes que entran a la unión es
igual a la suma de las corrientes que salen de ella.
Ia – Ib – Ic = 0 ó Ia
= Ib + Ic
Segunda Ley: LEY DE VOLTAJES DE KIRCHHOFF: "La suma algebraica de
las diferencias de potencial alrededor de cualquier trayectoria cerrada en un
circuito es cero".
Esto
significa que en un circuito cerrado, la suma de las elevaciones de tensión es
igual a la suma de las caídas de tensión.
V1 - V2 - V3 = 0 ó V1 = V2 + V3
Resistencias de carbón (varias
ver diagrama)
1)
a) Examine
el circuito de la figura 9-3. Realice los cálculos que se piden.
b) Conecte el circuito de la figura 9-3. Use el voltaje de la fuente (V) a 9 V. Mida y
anote:
Valores Calculados:
|
Valores Medidos:
|
Porcentaje de error:
|
V = _____________
|
V = _____________
|
% e = ____________
|
I1 = _____________
|
I1 = _____________
|
% e = ____________
|
I2 = _____________
|
I2 = _____________
|
% e = ____________
|
I3 = _____________
|
I3 = _____________
|
% e = ____________
|
I4 = _____________
|
I4 = _____________
|
% e = ____________
|
c)
Calcule el porcentaje de error.
d) Anexe sus cálculos al final de la práctica.
2) a) Examine el circuito de la figura 9-4. Realice los
cálculos que se piden.
b) Conecte el circuito de la figura 9-4. Use el voltaje de
la fuente (V) a 9 V. Mida y anote:
Valores Calculados:
|
Valores Medidos:
|
Porcentaje de error:
|
V = _____________
|
V = _____________
|
% e = ____________
|
I = _____________
|
I = _____________
|
% e = ____________
|
V1 = _____________
|
V1 = _____________
|
% e = ____________
|
V2 = _____________
|
V2 = _____________
|
% e = ____________
|
V3 = _____________
|
V3 = _____________
|
% e = ____________
|
c)
Calcule el porcentaje de error.
d) Anexe sus cálculos al final de la práctica.
3) a) Examine el circuito de la figura 9-5. Realice los
cálculos que se piden.
b) Conecte el circuito de la figura 9-5.Use el voltaje de la
fuente (V) a 9 V. Mida y anote:
Valores Calculados:
|
Valores Medidos:
|
Porcentaje de error:
|
V = _____________
|
V = _____________
|
% e = ____________
|
V1 = _____________
|
V1 = _____________
|
% e = ____________
|
V2 = _____________
|
V2 = _____________
|
% e = ____________
|
V3 = _____________
|
V3 = _____________
|
% e = ____________
|
I1 = _____________
|
I1 = _____________
|
% e = ____________
|
I2 = _____________
|
I2 = _____________
|
% e = ____________
|
I3 = _____________
|
I3 = _____________
|
% e = ____________
|
a) Examine el circuito de la figura 9-6. Realice los cálculos que se
piden.
b) Conecte el circuito de la figura 9-6. Use el voltaje de
la fuente (V) a 9 V. Mida y anote:
Valores Calculados:
|
Valores Medidos:
|
Porcentaje de error:
|
V = _____________
|
V = _____________
|
% e = ____________
|
V2 = _____________
|
V2= _____________
|
% e = ____________
|
V3 = _____________
|
V3= _____________
|
% e = ____________
|
V5= _____________
|
V5 = _____________
|
% e = ____________
|
V6= _____________
|
V6= _____________
|
% e = ____________
|
I1 = _____________
|
I1 = _____________
|
% e = ____________
|
I2 = _____________
|
I2 = _____________
|
% e = ____________
|
I3 = _____________
|
I3 = _____________
|
% e = ____________
|
I4 = _____________
|
I4 = _____________
|
% e = ____________
|
I5= _____________
|
I5= _____________
|
% e = ____________
|
I6= _____________
|
I6= _____________
|
% e = ____________
|
I7= _____________
|
I7= _____________
|
% e = ____________
|
c)
Calcule el porcentaje de error.
d) Anexe sus cálculos al final de la práctica.
Práctica # 10
MÉTODO DE NODOS
1. Verificar experimentalmente el método de nodos para el análisis de
circuitos.
El análisis de redes eléctricas por nodos es un método que utiliza la
Ley de Corrientes de Kirchhoff para obtener un conjunto de ecuaciones
simultáneas que, al ser resueltas, suministran la información concerniente a
los voltajes a través de cada elemento de circuito.
Un nodo es un punto de unión de dos o más elementos de circuito. Si en
un nodo se unen más de tres elementos, tal nodo se llama Nodo Mayor o
Principal. El número de ecuaciones de nodos es igual al número de nodos mayores
menos uno. Por lo tanto, cuando se seleccionan los nodos mayores, se omite el
nodo que conecta el mayor número de ramas, ya que se considera como nodo de
referencia y se le asigna un voltaje igual a cero.
El circuito que se muestra en la figura 5-1 se utilizará como guía para
el desarrollo de la técnica de análisis por nodos.
Note que los nodos mayores han sido numerados.
Llamaremos
V a la diferencia de potencial o voltaje entre el nodo 1 y el nodo 3, que es el
nodo que tomaremos como referencia, con la referencia positiva en el nodo 1, y
V al voltaje entre el nodo 2 y el mismo nodo de referencia, con la referencia
positiva en el nodo 2. Aplicando la Ley de Corrientes de Kirchhoff, obtenemos
las siguientes ecuaciones:
Para el nodo 1: I1 = IR1
+ IR2
Donde (V1 – V2) representa la diferencia de
potencial entre los nodos 1 y 2.
El siguiente
paso sería resolver las ecuaciones, por cualquier método de solución de
ecuaciones simultáneas, para obtener los valores de los voltajes de los nodos.
Resistencias de diferentes valores: (vea Fig. 10-2)
1. a) Examine el circuito de la figura 9-2. Obtenga las
ecuaciones de nodos y calcule los voltajes. Anexe los cálculos al final de la
práctica.
Fig. 10-2
b) Conecte el circuito de la figura 9-2. Mida y anote:
Valores calculados:
|
Valores medidos:
|
Porcentaje de error:
|
V1= ___________
|
V1= ___________
|
% e = _________
|
V2= ___________
|
V2= ___________
|
% e = _________
|
c) Con los voltajes obtenidos de las ecuaciones de nodos,
calcule el voltaje en cada una de las resistencias. Note que los valores de
resistencia se tomaron en el orden que aparecen en la figura, empezando por la
izquierda. Anexe también estos cálculos.
Valores calculados:
|
Valores medidos:
|
Porcentaje de error:
|
V220Ω= ___________
|
V220Ω= ___________
|
% e = _________
|
V330Ω= ___________
|
V330Ω= ___________
|
% e = _________
|
V470Ω= ___________
|
V470Ω= ___________
|
% e = _________
|
V100Ω= ___________
|
V100Ω= ___________
|
% e = _________
|
V330Ω= ___________
|
V380Ω= ___________
|
% e = _________
|
e) Calcule los porcentajes de error.
f) ¿Qué puede decir de los voltajes en las resistencias con
respecto a los voltajes en los nodos?
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
_____________________________________________________________________________________
2. a) Examine el circuito de la figura 10-3. Obtenga las ecuaciones de
nodos y calcule los voltajes. Anexe los cálculos al final de la práctica.
FIG.
10-3
2. a) Examine el circuito de la figura 10-3. Obtenga las ecuaciones de
nodos y calcule los voltajes. Anexe los cálculos al final de la práctica.
b) Conecte el circuito de la figura 10-3. Mida y Anote:
Valores calculados:
|
Valores medidos:
|
Porcentaje de error:
|
V1= ___________
|
V1= ___________
|
% e = _________
|
V2= ___________
|
V2= ___________
|
% e = _________
|
V3= ___________
|
V3= ___________
|
% e = _________
|
c) Con los voltajes obtenidos de las ecuaciones de nodos, calcule el voltaje en cada una de las resistencias. Anexe también estos cálculos.
Valores calculados:
|
Valores medidos:
|
Porcentaje de error:
|
V220 Ω = ___________
|
V220 Ω = ___________
|
% e = _________
|
V50Ω= ___________
|
V50 Ω = ___________
|
% e = _________
|
V150Ω= ___________
|
V150Ω= ___________
|
% e = _________
|
e) Calcule los porcentajes de error.
_ ________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
2. ¿Cómo se obtienen más fácilmente las ecuaciones de nodos,
con conductancias o con resistencias?¿Por qué?
_ _________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
_ _________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
______________________________________________________________________________________
___________________________________________________________________________________________
___________________________________________________________________________________________
MÉTODO DE MALLAS
1. Verificar experimentalmente el
método de mallas para el análisis de circuitos.
El análisis de redes eléctricas por mallas es un método que
utiliza la Ley de Voltajes de Kirchhoff
para obtener un conjunto de ecuaciones simultáneas que permitan determinar
los valores de las corrientes que pasan por las ramas del circuito en estudio.
El método de mallas se puede usar sólo en redes planas, es
decir, que sea posible dibujar el diagrama del circuito en una superficie plana
de tal forma que ninguna rama quede por debajo o por encima de ninguna otra.
Se define una malla como un lazo, o trayectoria cerrada, que
no contiene ningún otro lazo dentro de él, y una corriente de malla como
aquélla que circula sólo alrededor del perímetro de una malla
Se
utilizará el circuito que se muestra en la figura 10-1 para ilustrar la técnica
de análisis por mallas.
Note que se indican las corrientes de malla como I1 e I2 con la dirección que concuerda con la convención pasiva de los
signos. Aplicando la Ley de Voltajes de Kirchhoff, se obtienen las siguientes
ecuaciones:
Para la malla 1: V1 –
R1(I1) – R2(I1 +I2)
Donde (I1 + I2) es la corriente que
circula por la resistencia R2.
Ordenando: V1 = (R1 + R2) I1
+R2 I2
Para la malla 2: V2 =R2I2 +R2(I1
+I2)
Ordenando: V2 = R2I2 +(R2
+R3)I2
El
siguiente paso es resolver las ecuaciones, por cualquier método de solución de ecuaciones
simultáneas, y obtener los valores de las corrientes de malla.
Resistencias de: 50Ω, 100Ω,
150Ω, 220Ω, 330Ω, 470Ω.
2 Fuentes de alimentación
1.
a) Examine el circuito de la figura 11-2. Obtenga las ecuaciones
de mallas y calcule las corrientes. Anexe los cálculos al final de la práctica.
Fig. 11-2
b) Conecte el circuito de la figura 11-2. Mida y anote:
Valores calculados:
|
Valores medidos:
|
Porcentaje de error:
|
I1= ___________
|
I1= ___________
|
% e = _________
|
I2= ___________
|
I2= ___________
|
% e = _________
|
c) Con las corrientes obtenidas de las ecuaciones de mallas,
calcule la corriente que circula por cada una de las resistencias. Anexe
también estos cálculos.
Valores calculados:
|
Valores medidos:
|
Porcentaje de error:
|
I220Ω= ___________
|
I220Ω = ___________
|
% e = _________
|
I50Ω = ___________
|
I50Ω = ___________
|
% e = _________
|
I150Ω= ___________
|
I150Ω = ___________
|
% e = _________
|
e) Calcule los porcentajes de error.
1.
a) Examine el circuito de la figura 11-3. Obtenga las ecuaciones
de mallas y calcule las corrientes. Anexe los cálculos al final de la práctica.
Fig.11-3
b) Conecte el circuito de la figura 11-3. Mida y Anote:
Valores calculados:
|
Valores medidos:
|
Porcentaje de error:
|
I1= ___________
|
I1= ___________
|
% e = _________
|
I2= ___________
|
I2= ___________
|
% e = _________
|
I3= ___________
|
I3= ___________
|
% e = _________
|
c) Con las corrientes obtenidas de las ecuaciones de mallas, calcule la
corriente que circula por cada una de las resistencias. Note que los valores de
resistencia se tomaron en el orden que aparecen en la figura, empezando por la
izquierda. Anexe también estos cálculos.
Valores calculados:
|
Valores medidos:
|
Porcentaje de error:
|
I220Ω= ___________
|
I220 Ω = ___________
|
% e = _________
|
I330Ω= ___________
|
I330Ω = ___________
|
% e = _________
|
I470Ω= ___________
|
I470Ω = ___________
|
% e = _________
|
I100Ω= ___________
|
I100Ω = ___________
|
% e = _________
|
I330Ω= ___________
|
I330Ω = ___________
|
% e = _________
|
e) Calcule los porcentajes de error.
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
__________________________________________________________________________________
___________________________________________________________________________________
__________________________________________________________________________________________
__________________________________________________________________________________________
__________________________________________________________________________________________
__________________________________________________________________________________________
__________________________________________________________________________________________
Práctica # 12
Constantes
de tiempo RC
1.-Determinar mediante experimentos el
tiempo que un capacitor tarda en cargarse
a través de una resistencia.
2.-Determinar mediante experimentos el
tiempo que un capacitor tarda en descargarse
a través de una resistencia.
La carga en coulomb Q, de un capacitor es
igual a la capacitancia, C, en faradios por el voltaje, V, en volts al que se
carga el capacitor. Es decir,
Q = C X V.
El tiempo requerido para cargar un capacitor hasta el 63.2 % (aproximadamente) del
Voltaje aplicado se llama constante de
tiempo. (ơ)
Cuando un capacitor de C faradios se carga
a través de una resistencia de R Ohms,
la constante de tiempo, ơ, en segundos del circuito de carga es
ơ = R X C.
En cualquier instante durante la carga de
un capacitor, el voltaje activo, Va, es
igual a la diferencia entre el voltaje de la fuente, E, y
el voltaje en el capacitor; esto es,
Son necesarias cinco constantes de tiempo
para que un capacitor se cargue al 99 %
(aproximadamente) del voltaje aplicado
Cuando un capacitor de C faradios se descarga
a través de una resistencia de R ohms,
la constante de tiempo, ơ, en segundos del circuito de descarga es ơ = R X C.
Se dice que en cinco constantes de tiempo
el capacitor está totalmente descargado.
Una constante de tiempo es una medida
relativa no absoluta
Se considera un circuito
RC a todo aquel circuito compuesto: de una
resistencia, condensador y fuente
Figura12-1. Circuito
RC
Un capacitor es un dispositivo
que al aplicársele una fuente de alimentación de corriente continua se comporta
de una manera especial.
Cuando el
interruptor se cierra, la corriente I aumenta bruscamente a su valor máximo
como un cortocircuito) y tiene el valor de I
= E / R amperios (como si el capacitor no existiera momentáneamente en este
circuito RC), y poco a poco esta corriente va disminuyendo hasta tener un valor
de cero.
El voltaje en el
capacitor no varía instantáneamente y sube desde 0 voltios hasta E voltios (E
es el valor de la fuente de corriente directa conectado en serie con R y C).
Un condensador en
un circuito RC serie no se descarga inmediatamente cuando es desconectado de
una fuente de alimentación de corriente directa Cuando el interruptor pasa de
la posición A a la posición B, el voltaje en el condensador Vc empieza a
descender desde Vo (voltaje inicial en el condensador) hasta tener 0 voltios de
la manera que se ve en el gráfico inferior.
La corriente
tendrá un valor máximo inicial de Vo/R y la disminuirá hasta llegar a 0
amperios.
La corriente que
pasa por la resistencia y el condensador es la misma. Acordarse que en un
circuito en serie la corriente es la misma por todos los elementos.
·
Interruptor
un polo dos tiros
·
Resistencia
de 100kΩ y cables de conexión.
PROCEDIMIENTO
EXPERIMENTAL
a)
Armar circuito RC de acuerdo a la figura 12-6 mostrada abajo,
una vez armado mantener el interruptor en la posición de
abierto y con el capacitor descargado
b) Establecemos
el voltaje de la fuente a 9 voltios.
c) Se pone el interruptor en la posición a y se toma la lectura del amperímetro
cada 5 segundos, una vez que pasaron 65 segundos se pasa el interruptor a la posición b y se toma las lecturas del voltímetro igual que como se
realizó con el amperímetro.
d) Una vez
tomadas las mediciones directas del voltímetro y amperímetro se llena la tabla
12-1 de datos.
e) Se realiza el gráfico I vs t y V vs t, para calcular el
valor de τ mediante el uso de ambos
gráficos. Luego se obtiene el gráfico linealizado para I vs t y V vs t y
se calcula el valor de la constante de
tiempo τ de forma más formal y este es el que se usa para el cálculo de los errores, ya que el
valor teórico es τ=RC.
Tabla 12-1 Registre los valores de
voltaje y corriente para los procesos de carga y descarga del capacitor
Tiempo (segundos)
|
Corriente
(μ amperios A)
|
Voltaje
(voltios V)
|
0,0
|
|
|
5,0
|
|
|
10,0
|
|
|
15,0
|
|
|
20,0
|
|
|
25,0
|
|
|
30,0
|
|
|
35,0
|
|
|
40,0
|
|
|
45,0
|
|
|
50,0
|
|
|
55,0
|
|
|
60,0
|
|
|
65,0
|
|
|
-
Constante
del tiempo experimental
-
Diferencia entre el valor teórico y el
valor experimental de la constante de tiempo
Datos del capacitor y resistencia
1.- Dibuja en el papel cuadriculado los datos obtenidos al aplicar la fórmula de
carga de un capacitor (usa color azul para la curva)
2.- Con los
datos obtenidos del cuadro de la carga real dibuja en la misma hoja anterior la
curva de carga real pintándola de rojo.
3.- Dibuja
en otra hoja cuadriculada las dos curvas correspondientes a la Descarga Teórica
y a la Descarga Real, usando colores diferentes.
1.
¿Por qué la expresión de la corriente
en el capacitor cuando este se está descargando lleva el signo negativo?
____________________________________________________________________________________
____________________________________________________________________________________
____________________________________________________________________________________
3. Señale dos posibles fuentes de
errores que puedan haberse encontrado en la presente práctica.
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
4. Calcule la diferencia entre el
valor teórico y el valor experimental de al constante de tiempo.
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
5.
¿Qué es
un capacitor?
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
6.
¿Qué es
una constante de tiempo?
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
___________________________________________________________________________________
CONCLUSIONES:
___________________________________________________________________________________________
___________________________________________________________________________________________
___________________________________________________________________________________________
___________________________________________________________________________________________
___________________________________________________________________________________________
___________________________________________________________________________________________